么公要了我一晚上好大|热色综合|97碰视频|中文字幕一区二区三区在线不卡 |国产极品日韩极品欧美极品精品

  • 掃碼訪問網(wǎng)站

精英特速讀記憶訓(xùn)練軟件2.0版本已正式發(fā)布，有關(guān)“學(xué)員登錄”的各項(xiàng)功能已經(jīng)集成到訓(xùn)練軟件中，故網(wǎng)站上不再提供“學(xué)員登錄”。

請各位學(xué)員升級到新版本或重新安裝新版本軟件，以獲得更好的訓(xùn)練體驗(yàn)。

精英特手機(jī)版網(wǎng)站
注冊訓(xùn)練帳號
5,890,553
參加訓(xùn)練流程
即刻加入精英特速讀記憶訓(xùn)練！！！
您的瀏覽位置：首頁 >> 方法技巧 >> 常見的幾何輔助線口訣
常見的幾何輔助線口訣
    解幾何題，當(dāng)題目給出的條件不夠時，我們常通過添加輔助線構(gòu)成新圖形，形成新關(guān)系，使分散的條件集中，把問題轉(zhuǎn)化為自己能解決的問題，這便是輔助線的作用。但輔助線又因形態(tài)、用途等的不同而呈現(xiàn)出種類繁多，學(xué)業(yè)繁忙的學(xué)習(xí)們?nèi)绾斡米疃痰臅r間來快速記憶并熟練運(yùn)用這些輔助線呢？

    下面小編就給大伙分享一些常見的幾何輔助線口訣，它們讀起來朗朗上口，非常易于快閱讀和記憶，心動的學(xué)子可以趕緊運(yùn)用你手中的記憶方法來快速記憶吧！
 
    口訣1：注意點(diǎn)
 
    輔助線，是虛線，畫圖注意勿改變。假如圖形較分散，對稱旋轉(zhuǎn)去實(shí)驗(yàn)。基本作圖很關(guān)鍵，平時掌握要熟練。
    解題還要多心眼，經(jīng)常總結(jié)方法顯。切勿盲目亂添線，方法靈活應(yīng)多變。分析綜合方法選，困難再多也會減。
    虛心勤學(xué)加苦練，成績上升成直線。
 
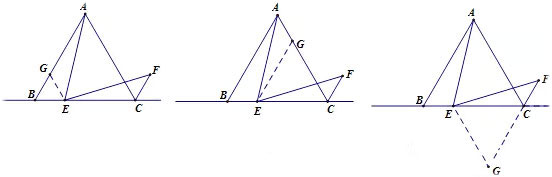
    口訣2：三角形
 
幾何輔助線口訣記憶——三角形的輔助線
 
    圖中有角平分線，可向兩邊作垂線。也可將圖對折看，對稱以后關(guān)系現(xiàn)。角平分線平行線，等腰三角形來添。
    角平分線加垂線，三線合一試試看。線段垂直平分線，常向兩端把線連。線段和差及倍半，延長縮短可試驗(yàn)。
    線段和差不等式，移到同一三角去。三角形中兩中點(diǎn)，連接則成中位線。三角形中有中線，延長中線等中線
 
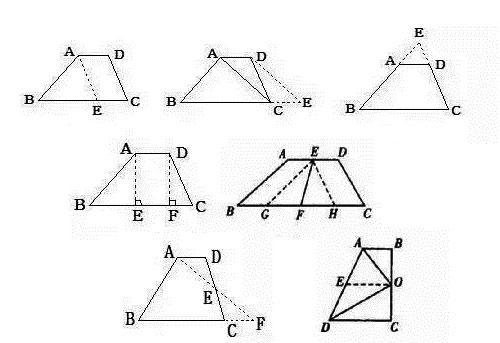
    口訣3：四邊形
 
幾何輔助線口訣記憶——四邊形的輔助線
 
    平行四邊形出現(xiàn)，對稱中心等分點(diǎn)。梯形問題巧轉(zhuǎn)換，變?yōu)椤餍魏汀跣巍Ｆ揭蒲茖牵瑑裳娱L作出高。
    如果出現(xiàn)腰中點(diǎn)，細(xì)心連上中位線。上述方法不奏效，過腰中點(diǎn)全等造。證相似，比線段，添線平行成習(xí)慣。
    等積式子比例換，尋找線段很關(guān)鍵。 直接證明有困難，等量代換少麻煩。斜邊上面作高線，比例中項(xiàng)一大片。
 
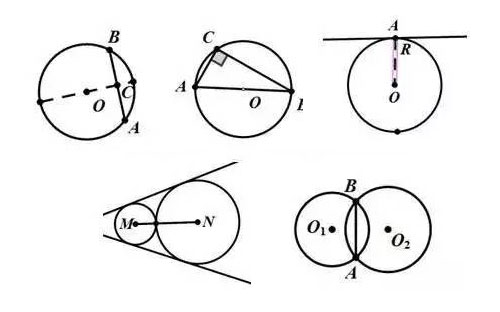
    口訣4：圓形
 
幾何輔助線口訣記憶——圓形的輔助線
 
    半徑與弦長計算，弦心距來中間站。圓上若有一切線，切點(diǎn)圓心半徑連。切線長度的計算，勾股定理最方便。
    要想證明是切線，半徑垂線仔細(xì)辨。是直徑，成半圓，想成直角徑連弦。弧有中點(diǎn)圓心連，垂徑定理要記全。
    圓周角邊兩條弦，直徑和弦端點(diǎn)連。弦切角邊切線弦，同弧對角等找完。 要想作個外接圓，各邊作出中垂線。
    還要作個內(nèi)接圓，內(nèi)角平分線夢圓。如果遇到相交圓，不要忘作公共弦。內(nèi)外相切的兩圓，經(jīng)過切點(diǎn)公切線。
    若是添上連心線，切點(diǎn)肯定在上面。要作等角添個圓，證明題目少困難。
 
    記住了這些口訣，再在平常的解題中多活學(xué)活用，必定能實(shí)現(xiàn)思維敏捷，正確率增加，尤其是在高考這樣的關(guān)鍵時刻，更能節(jié)約出大量時間來做其他題目或查錯，那些看似離你遙遠(yuǎn)的高分在熟記這些輔助線口訣后，就不會再是奢望了！

  精英特速讀記憶訓(xùn)練軟件：點(diǎn)此免費(fèi)下載試用


 
本欄目相關(guān)文章：
·學(xué)會“自問自答”，讓你不再害怕寫作！·語文考試時間不夠怎么辦？
·如何戰(zhàn)勝偏科，拉長學(xué)習(xí)中的短板·進(jìn)行有效預(yù)習(xí)，是提高成績的起點(diǎn)
·最有效的學(xué)習(xí)方法：高效輸入+有效輸出·難以集中注意力？試試這5個方法
·有效學(xué)習(xí)的4個關(guān)鍵法則！·2個思維工具，助你培養(yǎng)成長型思維！
·看似懂了卻一做就錯，你需要知道這3個辦法！·要實(shí)現(xiàn)高效閱讀，就要學(xué)會在閱讀中抓住重點(diǎn)
·正確認(rèn)識幼兒閱讀，從小培養(yǎng)閱讀好習(xí)慣·怎么做課堂筆記，最好的方法是什么？
·讓知識記得又快又牢的5個秘訣！·遠(yuǎn)離學(xué)習(xí)中這5個低效陷阱，助你實(shí)現(xiàn)高效學(xué)習(xí)！
·費(fèi)曼學(xué)習(xí)法：以教促學(xué)·聰明人的3個標(biāo)準(zhǔn)，你都具備嗎？
·不同的書有不同的讀法，你都知道嗎？·新手如何開始寫作？來試試“自由書寫”！
·為什么要寫作？如何提高寫作的能力和水平？·做好這4點(diǎn)，從小培養(yǎng)孩子專注力
·了解真實(shí)的快速閱讀和快速記憶，避免上當(dāng)受騙！·如何實(shí)現(xiàn)高效自學(xué)？掌握這4個要訣就夠了！
·長時間專注做事的5個秘訣，幫你培養(yǎng)專注力！·萬萬沒想到：注意力可以這樣提升
·數(shù)字特征記憶法·集中注意記憶法
·提問式閱讀之于記憶的作用·為什么學(xué)習(xí)讓你精疲力竭？
·心想事成記憶法·培養(yǎng)語文抽象思維能力的3種有效途徑和6種實(shí)用方法
·幾個簡單又實(shí)用的速讀方法· 給大考將至、時間緊迫的你五條復(fù)習(xí)備考建議
·在預(yù)習(xí)和復(fù)習(xí)中要注意的幾個問題·六步雞血背單詞法： 10天背完4000個GRE單詞的神奇記憶法
·還在為偏科煩惱嗎？試試這套拯救方案！·如何把文章寫到讀者心里去？
·提升寫作能力的練筆“四定原則”·提高做事效率的3種高效時間管理方法
·避免把文章寫成“流水賬”的建議·幾種效果顯著的抗壓、減壓好技巧
·你想每天都精力充沛、活力滿滿、表現(xiàn)出色嗎？你得學(xué)會管理自己的精力！·7個背誦英語的技巧
·快速閱讀中的時間管理-拖延癥·給想自學(xué)、又不得法的朋友們一些自學(xué)方法和經(jīng)驗(yàn)
·簡單又接地氣的2種專注力訓(xùn)練方法·風(fēng)靡全球的2種專注力訓(xùn)練方法
·幾種好用的學(xué)習(xí)筆記法·這14個方法，教你做一個情緒穩(wěn)定的人
·快速閱讀，一種不容忽視的能力·一種擁有“神奇功效”的筆記法
·如何在短期內(nèi)掌握陌生領(lǐng)域的知識？·移動筆記法
·如何畫魚骨圖？·累積微習(xí)慣的14個重要建議
·為什么你那么忙，卻沒有成效？你知道自己效率低下的原因嗎？·幾個讓你溝通更有效率的方法
·魏書生堅(jiān)持一生的6個時間管理法則·開學(xué)后孩子學(xué)習(xí)狀態(tài)不好怎么辦？15個建議幫孩子找到最佳學(xué)習(xí)狀態(tài)！
·如何改掉思想懶惰？·學(xué)會擁抱無聊，才能更加專注地工作和學(xué)習(xí)！
·讓自己心理變強(qiáng)大的兩種方法·掌握這些技巧，輕松戒掉壞習(xí)慣，養(yǎng)成好習(xí)慣！
·時間的3個秘密：如何通過“心流狀態(tài)”讓效率提高3~5倍？·從《反恐24小時》中學(xué)習(xí)時間管理
·培養(yǎng)深度工作和學(xué)習(xí)的能力，輕松提高自己的做事效率！·應(yīng)變思維能力訓(xùn)練
·怎樣做出一份引人注意的工作匯報PPT ·從這三個方向，去找到適合自己的學(xué)習(xí)方法
·成年人該如何提升專注力？·時間管理的一個大誤區(qū)：從起床開始做計劃
·倒背如流引發(fā)的記憶思考·拿到新課本，該怎么預(yù)習(xí)？
·學(xué)習(xí)=知識+實(shí)踐+思考+心態(tài)·堅(jiān)持是學(xué)習(xí)的最好方法
·考130分的人是怎么背單詞的？·觀察力好的學(xué)生有多開掛
·中小學(xué)生寒假須養(yǎng)成的9個好習(xí)慣·一個人越來越厲害的3種思維工具
·整體式學(xué)習(xí)法·怎么培養(yǎng)我們的觀察力？
·緩解眼睛疲勞最簡單的幾個方法·明確自己的時間使用效率，目標(biāo)計劃才能順利達(dá)成！
·操作性最強(qiáng)的學(xué)習(xí)方法·我就這樣擺脫了“三心二意”
·精英特速讀教會我站在高處閱讀·怎樣克服閱讀拖延癥？
·摒除雜念的九個方法·六招助你創(chuàng)意無限
·10個提高解決問題能力的方法·增加注意力的小技巧—觀察自己的呼吸
·六種不同階段的高效復(fù)習(xí)方法，助你期末復(fù)習(xí)備考事半功倍·4種讓時間多出1倍的方法
·怎樣提高注意力（4）：積極思考·怎樣提高注意力（3）：動態(tài)畫面
·怎樣提高注意力（2）：情感沖擊·怎樣提高注意力（1）：注意力受我們的內(nèi)心所掌控
·如何建立自己的知識體系，把學(xué)到的知識系統(tǒng)化，更好地掌握知識？·六步循環(huán)法：讓你沒有做不成的事
·最好用的學(xué)習(xí)進(jìn)步神器：錯題本·過度記憶法
·一線教師總結(jié)：18種改善期末學(xué)習(xí)動力不足的方法·避免盲目堅(jiān)持的10個實(shí)用方法
·給思維跳躍者的10個建議·減少網(wǎng)絡(luò)成癮的10個訣竅
·五步學(xué)習(xí)法·培養(yǎng)一種新習(xí)慣的7個小貼士
·如何對自己的學(xué)習(xí)和生活充滿激情？·你寫的“讀后感”，屬于哪一層？
·4種常用的知識輸出方法·你是想得太多還是在分析問題？
·戰(zhàn)勝自我挫敗的7個建議·3個方法教你學(xué)會如何學(xué)習(xí)，提高自主學(xué)習(xí)的效率！
·兒童注意力特點(diǎn)及訓(xùn)練方法·睡前的 9 條學(xué)習(xí)建議
·提高學(xué)習(xí)效率的43個小技巧·學(xué)習(xí)和工作中常用的幾種快速閱讀技巧
·總是容易分心？來測一測你是哪種注意力缺失者！·告別偽努力、減少浪費(fèi)時間、提升效率的36條學(xué)習(xí)建議
·七種讓閱讀速度飛起來的方法·養(yǎng)成一個新習(xí)慣，只要30天！
·13種觀察力訓(xùn)練法，給你一雙發(fā)現(xiàn)美的“眼睛”·鍛煉獨(dú)立思維的5個方法
·養(yǎng)成自學(xué)能力，要做到“四會”·針對不同學(xué)習(xí)材料的學(xué)習(xí)方法
·如何控制負(fù)面情緒？知乎超贊的方法~·寫作能力差？試試思維導(dǎo)圖法
·你的知識儲備越豐富，學(xué)習(xí)就會更輕松·遇到選擇就糾結(jié)？ 這些建議讓你做出更好決策
·抽象文字的趣味記憶方法——替換記憶法·我用這個方法，保證每天的清單任務(wù)被全部完成！
·提高專注力、高效率完成日常任務(wù)的3個方法·如何解決閱讀時注意力不集中的問題？
·節(jié)拍器訓(xùn)練法·8種超級視覺引導(dǎo)術(shù)，讓你擁有照相般的閱讀能力
·提升英語閱讀效率的3個訣竅·動作記憶法
·學(xué)習(xí)一項(xiàng)新技能時，必須經(jīng)歷的四個階段·閱讀理解記憶力的自測方法——復(fù)述
·學(xué)習(xí)能力強(qiáng)的人具有的八個特征·3461系統(tǒng)學(xué)習(xí)法
·一分鐘就可以學(xué)會的，提高閱讀速度2-3倍的方法：引導(dǎo)閱讀法·提高注意力的50種方法和技巧，總有一款適合你的！
·有這4個現(xiàn)象，說明你在做無效學(xué)習(xí)·快速閱讀訓(xùn)練法精選
·如何讓學(xué)習(xí)變成一件簡單輕松的事情？掌握這些方法和規(guī)律就夠了！·學(xué)習(xí)成績差怎么辦？7個技巧助你快速提高學(xué)習(xí)成績！
·初嘗PDCA循環(huán)學(xué)習(xí)法有感·比勤奮更重要的是學(xué)習(xí)力
·不想學(xué)習(xí)的時候，來看看這些方法吧！·快速閱讀相關(guān)：延長時間對效率的影響
·顛覆傳統(tǒng)的13條高效學(xué)習(xí)技巧·“萬能”高效學(xué)習(xí)方法，有沒有？
·你是什么性格，就用什么學(xué)習(xí)方法·掌握這三大步驟，幫你提高學(xué)習(xí)力，避免大腦遺忘
·為什么你總是要把事情拖到最后？·你是會講故事的人嗎？掌握這2個原則，你也能成為會講故事的人
·興趣記憶法·寫好記敘文的五個關(guān)鍵點(diǎn)
·一些幫你鍛煉反應(yīng)速度的方法·你為什么總是記不住？這里有8個方法，讓你讀得快，記得牢！
·一次就醫(yī)經(jīng)歷，讓我找到了提升效率的3個簡易方法·這九招讓你的目標(biāo)達(dá)成率提高3倍
·從“考王”梁實(shí)的高考中窺見方法的重要性·中學(xué)生的不當(dāng)學(xué)習(xí)方法及其對策
·21天真的可以養(yǎng)成一個好習(xí)慣，或戒掉一個壞習(xí)慣嗎？·神奇的睡眠學(xué)習(xí)法
·終身學(xué)習(xí)者的4個高效率自學(xué)習(xí)慣·怎么克服畏難心理、拖延癥以及懶惰？
·學(xué)霸們默認(rèn)的14個高分秘訣，趕快看·清華教授：你與學(xué)霸們拉開差距的，正是這4種學(xué)習(xí)能力
·6種最佳復(fù)習(xí)方法·用三個小習(xí)慣幫你找回專注力
·愛因斯坦和費(fèi)曼的“快速學(xué)習(xí)秘訣”·短時間讓自己成為學(xué)習(xí)高手的三個訣竅
·如何讓自己快速行動起來，走上轉(zhuǎn)變之旅？·4個改變“只收藏不閱讀”習(xí)慣的方法
·想要孩子閱讀速度快，一定要培養(yǎng)他的快速閱讀能力·一個考證牛人的5個考試秘籍
·賽博學(xué)習(xí)法·快速學(xué)習(xí)陌生領(lǐng)域的六大技巧
·3個迎考錦囊，送給高考倒計時的你·科學(xué)有效學(xué)習(xí)的16字訣
·衡水中學(xué)的9大學(xué)習(xí)方法·高中語文復(fù)習(xí)方法有講究，快速速讀能力需重視
·記憶方法轉(zhuǎn)為實(shí)際應(yīng)用的困惑與思考·我的碎片化時間管理心得
·寫文章難？因?yàn)槟闳鄙偃N思維的轉(zhuǎn)變！·發(fā)散思維巧學(xué)詩詞之關(guān)鍵詞發(fā)散法
·發(fā)散思維巧學(xué)詩詞之關(guān)鍵詞提取法 ·掌握這些提高記憶力的小竅門，備考事半功倍
·不會閱讀比不閱讀更可怕——中學(xué)生如何有效閱讀·如何自發(fā)自由自覺地學(xué)習(xí)？
·掌握速讀復(fù)習(xí)法，在哪考試都不怕·這四種筆記，你聽過嗎？
·時間管理中的“60-30-10法則”·速讀相關(guān)： 實(shí)踐“要事第一原則”的4個建議
·搭好比喻的“腳手架”，有助于學(xué)好晦澀抽象的知識·快速閱讀相關(guān)：2個節(jié)約時間的法則
·學(xué)習(xí)要講究方法，這些建議可以試試·寫好讀后感的“四字訣
·我在提升寫作能力過程中遇到的那些事·提高提問質(zhì)量的幾種方式
·利用好碎片時間，每天就能多出4小時！·為什么腦子里有很好的想法，卻寫不出來！或者寫不清楚？
·注意力實(shí)用訓(xùn)練技巧-顏色圖卡訓(xùn)練法·教你6個又快又好寫文章的實(shí)用方法
·怎樣不卡殼地寫出一篇文章？·注意力實(shí)用訓(xùn)練技巧—五分鐘靜坐冥想法
·5個方法助你建立一套良好的心態(tài)，打造自己的“成功腦”！·5種類型知識的記憶方法
·注意力實(shí)用訓(xùn)練技巧-舒爾特方格法·注意力實(shí)用訓(xùn)練技巧-固點(diǎn)凝視法
·有多個目標(biāo)想要實(shí)現(xiàn)時，該如何管理時間？·注意力集中訓(xùn)練六法，讓你做事全身心投入！
·高效執(zhí)行計劃的8個訣竅·全面學(xué)習(xí)金字塔法
· “華為人”的四大管理時間法寶·7個科學(xué)的記憶和學(xué)習(xí)方法
·不懂時間管理的人往往有這5個特點(diǎn)·用的人最少，效果最好的6個學(xué)習(xí)方法
·學(xué)好語文的一些訣竅·這五個方法，可以激勵你去主動學(xué)習(xí)
·提升日常工作效率的五點(diǎn)建議·有效提升學(xué)習(xí)效率的3種最強(qiáng)“學(xué)霸公式”
·怎么讓閱讀轉(zhuǎn)化成寫作？·7條提高你寫作水平的建議
·快速養(yǎng)成好習(xí)慣的4個步驟及11個方法·多輸出能讓記憶更牢固
·居家辦公&上網(wǎng)課的9個護(hù)眼小技巧·練習(xí)手指操20小時，提升閱讀速度28倍
·我常用這7個方法來提升專注力·精選記憶法
·教你使用思維導(dǎo)圖畫出你的目標(biāo)·改掉“抄和劃”，學(xué)會“寫和講”才能有效學(xué)習(xí)
·居家高效學(xué)習(xí)六法·低效能人士的七個習(xí)慣，你占幾個？
·有助效率工作的4種思考工具·護(hù)眼米字操
·高中英語語法的趣味口訣記憶法·疫情期間的宅家健康作息時間安排
·硅谷流行的MT時間管理術(shù)·用思維導(dǎo)圖整理并記住一本書的幾個步驟
·七個步驟，手把手教你制定并達(dá)成目標(biāo)·10種真正高效的學(xué)習(xí)方法
·猶太式輔導(dǎo)法·理解力的三個層次
·7個提升專注力的策略·“記憶力”不夠用，怎么辦？
·學(xué)習(xí)效率低的人不妨從這幾點(diǎn)開始改變·高效學(xué)習(xí)的七個偏方-怎樣學(xué)習(xí)更高效
·20條助你提升工作效率的時間管理技巧·幼兒注意力的培養(yǎng)方法
·訓(xùn)練過目不忘觀察力的超實(shí)用方法·A3學(xué)習(xí)法： 一個能讓人自由發(fā)揮的學(xué)習(xí)方法
·閱讀速度+閱讀技巧=高分閱讀·文章閱讀的六種能力與提高閱讀能力的五種方法
·期末復(fù)習(xí)提分最快的做法·快速閱讀中的心態(tài)管理—內(nèi)心平和
·考場中的快速閱讀方法·小學(xué)課內(nèi)外快速閱讀方法指導(dǎo)
·清華學(xué)霸談后天記憶力的培養(yǎng)方法·注意力不集中+拖延嚴(yán)重患者的自救措施
·快速閱讀相關(guān)：“別人家的孩子”你也可以做到！·應(yīng)付考試的三種常用記憶法
·晚自習(xí)時間這樣安排，學(xué)習(xí)效率最高·四環(huán)式記憶法
·中考散文的閱讀方法·如何使學(xué)生學(xué)會高效閱讀？
·六種高效學(xué)習(xí)策略·我親自實(shí)踐后，最有效的3個克服拖延癥的方法
·知識學(xué)完就忘？這些方法讓你高效復(fù)習(xí)！·如何通過閱讀自學(xué)一門新的技能？
·快速閱讀中的反拖延小技巧·8種科學(xué)有效的自考記憶技巧
·現(xiàn)代文考察的六種閱讀能力例談·woop思維，讓你擁有持續(xù)的行動力
·五種讓人欲罷不能的學(xué)習(xí)方法·記憶力差不要緊，知道這些，你也能有超強(qiáng)記憶力！
·怎樣補(bǔ)腦提高記憶力？·這些單詞記憶的誤區(qū)，你有嗎？
·培養(yǎng)習(xí)慣成功率翻倍的四條規(guī)則·成年人的閱讀方法及閱讀習(xí)慣漫談
·最好的學(xué)習(xí)，就是無意識的學(xué)習(xí)——英語學(xué)習(xí)經(jīng)驗(yàn)談·中學(xué)生學(xué)習(xí)方法雜談
·適用于提不起學(xué)習(xí)干勁的人：頭頂部意識集中法·他們都已書讀萬卷，我們還有什么理由不閱讀
·21天養(yǎng)成速讀習(xí)慣，寒門也能出貴族·從4個方面來做讀書筆記，讓讀書更有成效！
·學(xué)會便簽學(xué)習(xí)法，提升你的閱讀學(xué)習(xí)效率！·心智圖讓碎片化學(xué)習(xí)更有效
·提升效率的幾個小技術(shù)·時間與效率勵志故事二篇
·效率使用時間的六個建議·英語快速閱讀：閱讀理解丟分過多的分析
·你是哪種類型的拖延者？ ·左右腦協(xié)同記憶法
·博知記憶法·學(xué)生名字如何記得快用得好？——新學(xué)期教師必學(xué)技能
·文言文翻譯常用十二法·中學(xué)語文閱讀建議
·“付費(fèi)學(xué)習(xí)”是最簡單有效的學(xué)習(xí)方式·快速閱讀相關(guān)：吸引力法則讓你心想事成
·提問記憶法——學(xué)習(xí)和記憶效果最好的方法·記憶力相關(guān)：語文易混字詞及讀音的記憶
·快速閱讀相關(guān)：如何聰明的休息？·現(xiàn)代文閱讀：考試中閱讀速度太慢怎么辦？
·如何提高語文閱讀效率·“拼圖”與“登山”——中學(xué)與大學(xué)的學(xué)習(xí)方法
·快速閱讀中真正的專注是什么樣？·閱讀速度快不快，全靠閱讀筆記帶
·快速記憶化學(xué)元素符號六法·成為快速閱讀高手前要知道的幾件事
·快速閱讀相關(guān)：閱讀的433法則·想在速讀的路上越走越遠(yuǎn)，就別踩這兩個坑！
·精讀雅思閱讀的方法·這三個方法有助你消化吸收閱讀的內(nèi)容
·十種超實(shí)用的高效學(xué)習(xí)方法·情景記憶法
·省時又高效的復(fù)習(xí)方法·中學(xué)生閱讀中存在的幾個誤區(qū)
·中小學(xué)生如何提高期末復(fù)習(xí)效率？·提高英語閱讀能力好評度最高的九種技巧（中/英雙語）
·速讀相關(guān)：影響高效閱讀的幾個心理因素·速讀記憶相關(guān)：不是每件事都會立馬見效
·記憶大師的麻將牌記憶法·快速閱讀相關(guān)：“二八定理”在時間管理上的巧妙分配
·7位偉人的學(xué)習(xí)方法，看看哪款適合您·如何擺脫快速閱讀中的低水平勤奮（下）
·如何擺脫快速閱讀中的低水平勤奮(上)·流水線時間管理法
·高考寫出優(yōu)秀作文標(biāo)題的9個小技巧·高考前要改正的五個不良學(xué)習(xí)習(xí)慣
·七個思維體操·激發(fā)創(chuàng)造力的10個好點(diǎn)子
·高考理科復(fù)習(xí)必備的十個記憶方法·史上最全的高考語文閱讀題解題技巧
·記憶無序數(shù)字的最簡單方法·懶人的7種記憶方法
·說快速閱讀提升沒捷徑？對不起，是你不知道捷徑在哪里·適合快速閱讀的3種筆記法，總有一種合你意
·你對閱讀的理解對了嗎？·思維導(dǎo)圖與線性筆記的五大區(qū)別
·這4招告訴你什么才是科學(xué)的學(xué)習(xí)方法·掌握這3個關(guān)鍵點(diǎn)，輕松實(shí)現(xiàn)在碎片時間里快速閱讀
·快速閱讀相關(guān)：提升閱讀速度的9個策略·多閱讀是提高信息獲取能力的根本方法
·想要在速讀時提高理解力，可以關(guān)注這4個方面·提升孩子語文成績，要從這幾方面著手
·四種常用的快速閱讀技巧·清單思維讓你做事情更正確、更高效！
·訓(xùn)練有意注意的三種常見方法·手寫筆記依然是最好的記憶方式
·聲樂學(xué)習(xí)中的八種記憶方法·精讀、泛讀知多少？——快速閱讀后的思考
·為什么我要堅(jiān)持訓(xùn)練速讀？·幫你取得好成績的7種有效學(xué)習(xí)方法
·牛人的60條 “饑餓式”學(xué)習(xí)法·什么是視幅？如何擴(kuò)大視幅提高閱讀效率
·速讀記憶相關(guān)：測測你是個意志力堅(jiān)強(qiáng)的人嗎？ ·快速閱讀相關(guān)：業(yè)余時間關(guān)乎未來
·運(yùn)用遺忘曲線 讓復(fù)習(xí)更高效·我們該如何提高思考能力？
·學(xué)習(xí)的過程，就是建立新連接的過程！·12種消除音讀的方法
·快速閱讀相關(guān)：方法+行動=成功！·快速閱讀相關(guān)：可行性強(qiáng)的時間計劃讓學(xué)習(xí)碩果累累
·保持好奇心的七個方法·13個簡單有趣的單詞記憶方法
·最適合中國人的單詞記憶方法：拼音記單詞·把信息化繁為簡的神奇筆記術(shù)—子彈筆記
·提升快速閱讀能力的3個實(shí)用技巧·超級學(xué)習(xí)法
·成為“更聰明”學(xué)習(xí)者的三個方法·會分配精力 人生就像速讀一樣高效
·學(xué)習(xí) 時間 效果·蘇霍姆林斯基：大學(xué)生應(yīng)該怎么合理地利用在校時間？
·提高執(zhí)行力的三個小方法·小學(xué)數(shù)學(xué)中快速解題的6種“畫圖”法
·掌握這十個方法，你也可以學(xué)得很好·快速閱讀相關(guān)：如何快速歸納文章段意？
·新人必讀：文獻(xiàn)閱讀和管理經(jīng)驗(yàn)，學(xué)長傾囊相授·頂尖心理學(xué)家眼中提高兒童智力的7個方法
·《高潛》教你三招讓時間回報率翻倍·如何在閱讀中尋找自由切換工作、學(xué)習(xí)、生活的方法？
·3個小步驟竟讓我擺脫了半途而廢的“坑”·“增兵減灶法”一招幫你搞定拖延癥
·緩解眼睛疲勞的幾種辦法·16個高效英文閱讀技巧
·為什么讀了那么多的書，你還是不會時間管理？·管理時間的真諦在于管理自己
·8個被大部分人忽視的效率學(xué)習(xí)法！·人的注意力僅能維持8秒？3個保持注意力集中的科學(xué)方法
·三種日常生活和學(xué)習(xí)能用上的記憶方法·保持長時間高效學(xué)習(xí)的一些方法和建議
·怎樣讓大腦更年輕記憶力更好·七條少為人知的注意力秘籍讓你更專注
·用這些方法幫你告別“學(xué)習(xí)困難癥”·高三學(xué)生怎么提高記憶力？
·復(fù)習(xí)訣竅：只要17分鐘 ！讓記憶內(nèi)容一個月不忘·練就超強(qiáng)學(xué)習(xí)能力的七個方法
·高考必備：15條考場抓分技巧·改善青少年注意力小貼士
·教孩子識字的小竅門：別讓他看插圖·超高效記憶術(shù)：提升記憶力的三個方法
·四種快速學(xué)習(xí)方法·量化成本 三步戰(zhàn)勝拖延癥成為行動的巨人
·小學(xué)生口算能力培養(yǎng)六法·學(xué)會利用這15分鐘，讓你輕松告別拖延癥
·速讀記憶相關(guān)：成功的人那么多，為何偏偏不是你？·2018高考各科復(fù)習(xí)大全
·遠(yuǎn)離快速閱讀誤區(qū)，方能成為閱讀達(dá)人·學(xué)習(xí)時更容易集中注意力的四個建議
·速讀記憶相關(guān)：致探索的先驅(qū)者們！·自學(xué)時間不夠？試試想象學(xué)習(xí)法！
·速讀相關(guān)：四個步驟幫你建立一個新習(xí)慣·一位初中老師的語文提分大揭秘
·一個有趣的時間管理系統(tǒng)：把時間裝在桶里·11種好習(xí)慣讓你變得會學(xué)習(xí)
·速讀相關(guān)：十一條心理學(xué)建議助你減少焦慮·應(yīng)付一切考試的四個步驟——PCWC
·速讀記憶訓(xùn)練的“舍”與“得”·時間管理：每天3件事，開啟高效的一天
·中高考要改革？閱讀真的越來越重要了！·精英特教育博士談高中學(xué)習(xí)成功策略
·速讀記憶相關(guān)：十個增加學(xué)習(xí)動力的步驟·綜合記憶法
·5小時教你背會一首超長篇詩歌（下）·5小時教你背會一首超長篇詩歌（上）
·學(xué)習(xí)方法相關(guān)：漫談抄襲、改造與創(chuàng)新·新年新氣象：你的目標(biāo)要一步步走才會清晰（下）
·新年新氣象：你的目標(biāo)要一步步走才會清晰（上）·初中生如何豐富自己的作文語言
·只要6件事，就能找回孩子的專注力！·快速閱讀相關(guān)：2項(xiàng)法則讓你成功為自己增值
·英語閱讀滿分6字秘訣·橫向筆記才科學(xué)？
·自測記憶法·消除誤解，領(lǐng)略真正的快速閱讀之美
·十項(xiàng)自我控制意志力的策略·水平測試的4個速讀記憶小技巧
·速讀訓(xùn)練到底要不要跳級？·時間管理：簡單5步，讓你從此不賴床
·羅森塔爾效應(yīng)·學(xué)習(xí)效率與輔助工具的關(guān)系大不大？實(shí)例告訴你真相
·做好舒爾特表訓(xùn)練的幾個小技巧·找到你的專屬記憶類型，開啟過目不忘的記憶本領(lǐng)
·如何管理你的時間，就等于如何打理你的人生·分類閱讀是小學(xué)生做好語文閱讀的關(guān)鍵
·提升閱讀效率的十個注意點(diǎn)·淺談精英特背景音樂與專注力的關(guān)系
·高中階段進(jìn)行閱讀訓(xùn)練晚嗎？方法正確一樣有效！·13個開發(fā)大腦學(xué)習(xí)的技巧
·超級筆記術(shù)·邏輯思維能力的培養(yǎng)及測試方法
·你是在“假裝學(xué)習(xí)”嗎？·教你用100個數(shù)字巧記200條記憶內(nèi)容的方法（下）
·教你用100個數(shù)字巧記200條記憶內(nèi)容的方法（上）·淺談數(shù)字編碼法與家居定位法的取舍
·費(fèi)曼學(xué)習(xí)法·我的高效利用時間妙招（下）
·我的高效利用時間妙招（上）·五種學(xué)習(xí)力曲線
·為什么舒爾特表能有效提高注意力？·符號筆記法　
·晚上關(guān)掉手機(jī)可提高工作效率·如何培養(yǎng)小學(xué)生的閱讀素養(yǎng)
·找對姿態(tài)，輕松搞定文字舒爾特表·6個治愈“拖延癥“的藥方
·用“快準(zhǔn)狠”直接PK數(shù)字舒爾特表·學(xué)習(xí)的三層境界
·用娛樂式學(xué)習(xí)提高快速記憶的代入感·善用記憶力，高分輕松取
·“七多”學(xué)習(xí)法——學(xué)好高中語文的法寶·十種反拖延技巧
·記憶力差？從這4方面入手增強(qiáng)記憶力!·快速閱讀相關(guān)：提升能力要養(yǎng)成的五個好習(xí)慣
·淺談如何培養(yǎng)小學(xué)生的數(shù)學(xué)閱讀能力·快速閱讀相關(guān)：給你的閱讀“號號脈”
·小學(xué)生快速記憶生字的方法·保持愉悅的心態(tài)才能提高學(xué)習(xí)效率
·快速閱讀的綜合訓(xùn)練·小學(xué)生快速識字法
·六色熒光筆學(xué)習(xí)法——高效閱讀法·如何快速記憶元素周期表
·我們?yōu)槭裁匆淖冎鹱珠喿x的習(xí)慣·為什么我能用整體感知提升閱讀速度，你卻不行
·3個故事告訴你“消除音讀”究竟是什么樣子·把握幾個要點(diǎn)，讓您的小孩愛上閱讀
·中學(xué)生提高時間利用效率的四大原則·速讀相關(guān)：消除音讀之鋼琴師
·記憶術(shù)的七個心理元素·中學(xué)政治教材閱讀法
·享受速讀前奏樂：靜心調(diào)息·我從厭倦到迷戀上精英特速讀軟件僅用了七天
·培養(yǎng)想象力的四種途徑·五步輕松掌握濃縮學(xué)習(xí)法
·游戲與速讀·速讀相關(guān)：十招讓你擺脫枯燥學(xué)習(xí)的狀態(tài)
·親子閱讀中5個常見的的理解誤區(qū)及正確做法·“五覺”記憶法
·拖延癥計算公式·高中階段必須養(yǎng)成的四種能力
·速讀相關(guān)：有效訓(xùn)練是突破極限的最好方法·讓孩子學(xué)習(xí)亮起綠燈，只有精英特能辦到
·高考記憶法：物理光學(xué)和熱學(xué)的八大實(shí)用口訣·快速閱讀相關(guān)：改變閱讀習(xí)慣是一個過程
·我對速讀訓(xùn)練中標(biāo)藍(lán)字的思考·測測你的注意力集中程度
·如何找到屬于你的最佳學(xué)習(xí)方法·如何利用零散時間讀書
·五式思維訓(xùn)練法，激發(fā)你的備考潛能·快速閱讀相關(guān)：你是一個有學(xué)習(xí)力的人嗎？
·早起是時間管理的第一步·高效閱讀中影響注意力的7個因素
·備戰(zhàn)高考：一些調(diào)節(jié)復(fù)習(xí)疲勞的有效方法·提高思維能力：7種讓你變得更聰明的方法
·十個有效提高自制力的方法·詩詞更有助于速讀記憶能力的培養(yǎng)
·專家支招：中高考減壓必學(xué)三招兒·詩詞鑒賞“五步”走——怎樣鑒賞詩詞？
·快速閱讀相關(guān)：學(xué)速讀你要放下的8樣?xùn)|西·迎戰(zhàn)高考 選精英特就好
·豐富的課外閱讀是培養(yǎng)理解能力的保證·戰(zhàn)勝拖延癥的法寶：一盞茶的時間管理術(shù)
·如何開發(fā)智商？·時間管理：尋找精力與效率的平衡點(diǎn)
·快速閱讀是囫圇吞棗嗎？·中學(xué)生怎樣提高課外閱讀的質(zhì)量
·快速閱讀相關(guān)： 時間管理八法，哪個適合你？·快速閱讀相關(guān)：我們需要的是精讀還是速讀？
·快速閱讀相關(guān)：如何精讀？怎樣精讀更有效·速讀小技巧：“過電影”復(fù)習(xí)法
·小學(xué)生如何克服不良閱讀習(xí)慣？·快速閱讀訓(xùn)練中的理解率為什么是70% ?
·速讀相關(guān)：時間管理的幾個關(guān)鍵理念·蘇霍姆林斯基：如何發(fā)展青少年的記憶力
·快速閱讀相關(guān)：如何培養(yǎng)速讀的自學(xué)能力？·高效學(xué)習(xí)法——如何預(yù)習(xí)？
·“四字訣”助你輕松記憶高中自然地理·初學(xué)者學(xué)習(xí)速讀記憶要從學(xué)習(xí)方法開始
·學(xué)習(xí)是一件簡單的事——愛因斯坦談學(xué)習(xí)方法·我是怎樣在日常閱讀中培養(yǎng)快速閱讀習(xí)慣的
·為什么精英特速讀訓(xùn)練能“消除音讀”？·中外名人關(guān)于自律的名人名言
·快速閱讀相關(guān)：自律是快速閱讀成功的前提·高中數(shù)學(xué)單選題的十大提分方法
·高中語文高效記憶方法·淺談有效提高學(xué)生課外閱讀能力的方法
·為什么視幅擴(kuò)展和節(jié)奏訓(xùn)練時不許眨眼？·快速閱讀要努力才有回報
·神奇的記憶力要從培養(yǎng)觀察能力開始·幾種預(yù)防健忘癥的方法
·超級復(fù)習(xí)法 ·速讀記憶相關(guān)：學(xué)思并行 效率倍增
·想象和聯(lián)想是提高閱讀能力的有效方法·中外關(guān)于記憶的名人名言
·注意力不集中？跟專注的人呆一起！·速讀時代 學(xué)習(xí)力即未來
·培養(yǎng)想像力的六個原則·快速閱讀相關(guān)：如何成為一個知識淵博的人
·價值2.5萬美金的時間管理方法——六點(diǎn)優(yōu)先工作制·八種鍛煉最強(qiáng)大腦的方法
·思維導(dǎo)圖是手繪還是電腦繪制更好·快速閱讀相關(guān)：從名人的日常作息規(guī)律看快速閱讀習(xí)慣的養(yǎng)成
·提升閱讀效率從改掉“逐字閱讀“習(xí)慣開始·快速閱讀相關(guān)：改變閱讀習(xí)慣要多一點(diǎn)“耐心”
·淺析 “學(xué)習(xí)動機(jī)”與“學(xué)習(xí)效率”的關(guān)系·英語快速閱讀：詞匯量是托福閱讀考試的生命線
·快速閱讀相關(guān)：時間管理的誤區(qū) 你有幾個？·6種呼吸法助你提高閱讀速度
·快速閱讀中的節(jié)奏訓(xùn)練方法·集中注意力的十大秘訣
·學(xué)習(xí)思維導(dǎo)圖要注意四個“度”·記憶力相關(guān)：生活細(xì)節(jié)改善記憶力
·漢字聯(lián)想記憶五法·快速閱讀相關(guān)：有這13個特點(diǎn)的書閱讀起來更快
·快速閱讀技巧——五步速讀法·“整體感知”到底感知些什么？
·幾種簡單有效的觀察力訓(xùn)練方法·快速閱讀技巧之略讀的策略
·思維的基本方法及協(xié)調(diào)訓(xùn)練·淺談?wù)Z文學(xué)習(xí)習(xí)慣的養(yǎng)成
·從高考新大綱看快速閱讀習(xí)慣養(yǎng)成的重要性·高考語文文言文閱讀答題技巧
·不同年齡段人群的閱讀方法·精英特是網(wǎng)絡(luò)時代的大腦充電器
·快速閱讀相關(guān)：名人惜時如命的小故事·快速閱讀相關(guān)：影像閱讀給了我三件法寶
·快速閱讀，給自己一個變強(qiáng)的機(jī)會·歌訣記憶法
·王衍行：快速閱讀是金融高管取勝的利器·檢驗(yàn)?zāi)阌袥]有讀懂一本書的方法
·時間管理：上班族如何利用碎片化時間來閱讀？·經(jīng)驗(yàn)分享：我是如何提高閱讀和觀影時的記憶力的！
·快速閱讀之讀與寫·快速閱讀要去除三毒
·巧用閱讀目的助你縮短閱讀時間·提升孩子學(xué)習(xí)能力 選“精英特”就夠了
·李希貴：我是怎么引導(dǎo)兒子愛上閱讀的！·我對精英特軟件中“自選文章”的一些思考
·淺析精英特中的5個”速讀訓(xùn)練“認(rèn)知誤區(qū)·英語快速閱讀：五招輕松搞定SAT閱讀
·快速閱讀相關(guān)：閱讀時遇到困惑的11種應(yīng)對方法·快速閱讀，先要將閱讀當(dāng)成一種習(xí)慣
·快速閱讀的“分化論”和“為師論”·快速閱讀的“二重奏”
·快速閱讀相關(guān)：你知道如何提高盲生快速閱讀能力嗎？·哈佛學(xué)霸的高效時間管理技能
·思維導(dǎo)圖與知識結(jié)構(gòu)圖有什么不同？·快速閱讀相關(guān)：怎樣打好速讀訓(xùn)練的根基？
·英語快速閱讀：雅思閱讀部分時間安排技巧·克服閱讀疲勞的幾大要點(diǎn)和方法
·培養(yǎng)終身閱讀習(xí)慣的10個方法·快速閱讀當(dāng)似蝴蝶一般輕盈 如蜜蜂一樣蜇刺
·速讀訓(xùn)練相關(guān)：教你快速看3D圖的方法·學(xué)習(xí)快速閱讀要具備三大品質(zhì)
·你知道如何閱讀一本實(shí)用性的書籍么？·全腦速讀記憶都適用于哪些范圍或者領(lǐng)域？
·幾種提高英語學(xué)習(xí)和記憶力的高效方法·速讀相關(guān)：番茄工作法
·進(jìn)入高效學(xué)習(xí)狀態(tài)的9個特征·快速閱讀相關(guān)：學(xué)會“辨體”才能有效提高閱讀效率
·家長必讀：著名主持人培養(yǎng)孩子良好記憶習(xí)慣的經(jīng)驗(yàn)分享·快速閱讀相關(guān)： 我們應(yīng)該樹立什么樣的學(xué)習(xí)態(tài)度？
·快速閱讀技巧非一朝一夕之功·丹田呼吸時如何做到吸氣呼氣的時間為1：2？
·快速閱讀訓(xùn)練中眼球轉(zhuǎn)不快怎么辦？·高效復(fù)習(xí)五字訣
·快速閱讀 從“一”到“萬”的蛻變·get新技能：精英特助你擁有安迪一樣的閱讀速度
·改錯記憶法·必讀：尖子生的十個高效聽課技巧
·家長如何幫助孩子提高閱讀能力？·初中語文高分之“閱讀修煉篇”
·加古德次的30分鐘超級速讀訓(xùn)練法·速讀記憶相關(guān)：如何提高智力？
·兩種高效消除音讀的訓(xùn)練方法·瘋狂閱讀應(yīng)該如何把握？
·閱讀到位，還怕高考嗎？·精英特教你釋放潛能的方法
·14種增強(qiáng)記憶力的基本技巧·執(zhí)業(yè)藥師之藥理學(xué)的記憶技巧
·家長如何幫助孩子提高學(xué)習(xí)興趣· 七大技巧幫你改掉高考復(fù)習(xí)中愛走神的毛病
·感悟記憶術(shù)訓(xùn)練中的技法與技巧的本質(zhì)差異·從《荀子·勸學(xué)篇》探索記憶與學(xué)習(xí)之法
·影像閱讀法的基本閱讀步驟·快速閱讀之五絕論
·快速閱讀中快速克服“音讀/默讀“的四種方法·李開復(fù)：如何管理時間？
·你一定不知道是這八個因素拖了你的閱讀速度！·我是如何用思維導(dǎo)圖找到自己喜歡的工作的？
·加強(qiáng)閱讀效果的四種讀書筆記·畢業(yè)論文的好幫手——精英特速讀記憶軟件
·生活中有效防止記憶力衰退的7個方法·說明文的4種閱讀方法
·一個文科生的速讀識記苦惱·曼陀羅思考法
·快速學(xué)習(xí)的三種境界－－法、術(shù)、道·怎樣增加學(xué)習(xí)的動力？
·快速閱讀，從自身的作息說起·從李嘉誠的創(chuàng)業(yè)之路看快速閱讀的成功要素
·快速閱讀訓(xùn)練相關(guān)：超覺靜思法·教你幾招快速記憶抽象文字的方法
·我用這4種方法，讓女兒愛上閱讀和寫作·在教學(xué)過程中如何培養(yǎng)學(xué)生的多項(xiàng)閱讀能力？
·無聲速讀技巧—克服“四動”·十個良好的的學(xué)習(xí)習(xí)慣
·六種常用的聯(lián)想記憶法·一些鍛煉眼球靈活性與敏捷性的方法
·兩組簡單的健腦操 一學(xué)就會·快速閱讀是可以練成的—故事啟示篇
·快速閱讀訓(xùn)練中緩解眼睛疲勞的三種食物·快速記憶“九九乘法表”的方法
·精英特軟件中“舒爾特表”的訓(xùn)練方法和技巧·由快速閱讀訓(xùn)練談培養(yǎng)自信的方法
·提高記憶效果最有用的七大方法·快速閱讀似春風(fēng)
·七大閱讀法助你成為一個學(xué)富五車的人·10種提高文章理解力的方法
·抄寫記憶法·多樣閱讀法豐富了我的大學(xué)生活
·語文老師給我介紹的幾個提高閱讀速度的方法·10種常用的文章背誦法
·速讀記憶相關(guān)：我的高效閱讀方法總結(jié)·小學(xué)語文閱讀題型與答題方法大總結(jié)
·快速閱讀相關(guān)：三步突破閱讀速度瓶頸·快速閱讀相關(guān)：培養(yǎng)速讀能力，提高語文成績
·快速閱讀相關(guān)：如何培養(yǎng)學(xué)生的閱讀遷移能力？·快速閱讀與系統(tǒng)記憶
·快速閱讀方法雜談·高效學(xué)習(xí)法之”西蒙學(xué)習(xí)法”
·高效學(xué)習(xí)小技巧之“適當(dāng)休息”·中學(xué)數(shù)學(xué)常用的10種解題方法
·記憶七要訣·美國教育培養(yǎng)孩子想象力的七個原則
·如何用冥想導(dǎo)出α波 ？ ·閱讀要像庫里練就控球技術(shù)一樣扎實(shí)
·快速閱讀相關(guān)：習(xí)慣的力量·快速記憶相關(guān)： SAT詞匯八大記憶法
·速讀記憶相關(guān)：速讀離不開記憶·經(jīng)驗(yàn)分享：讓閱讀變得有趣的3個小方法
·閱讀要學(xué)會質(zhì)、速并行·物理常見記憶法
·提高材料閱讀效率的三大方法·閱讀速度是在潛移默化中提升的
·教你一些快速集中注意力的方法·提升閱讀速度的前提是要有足夠的閱讀量
·我提升閱讀效率的六個小方法·快速閱讀的兩大要素分析
·專訪“世界記憶之父“—托尼·博贊：“減輕壓力記憶力會越來越好”·快速緩解腦疲勞的幾個小動作
·我的讀書技巧·速讀速算能力可在玩耍中輕松學(xué)會
·快速閱讀相關(guān)：教你如何用兩小時看完一本書·如何提升您的閱讀速度和記憶力
·找對方法，“最強(qiáng)大腦”你也可以擁有·提高語文閱讀能力的十六字訣法
·多閱讀可提高記憶力·你是哪種類型的學(xué)習(xí)者？
·考研英語閱讀百日沖刺技巧：快、準(zhǔn)、狠！·五個方法教你區(qū)分思維導(dǎo)圖和知識樹
·珍惜時間：一分鐘能做什么事？·讓孩子愛上閱讀最簡單有用的幾個方法
·記憶力相關(guān)：簡單、高效的會計財經(jīng)法規(guī)與職業(yè)道德記憶法·我來告訴你該如何速記！
·你分得清思維導(dǎo)圖和概念圖嗎？·父母必讀：六大改善孩子記憶力的措施
·時間管理： 34枚金幣時間管理法 教你戰(zhàn)勝拖延癥！·精英特教你快速記憶英語音標(biāo)的方法
·這樣提高快速記憶力，別說我不告訴你！·英語閱讀技巧：六大標(biāo)點(diǎn)符號的作用匯總
·連續(xù)分段時間管理法·看學(xué)霸是怎樣養(yǎng)成閱讀習(xí)慣的！
·這些速讀技巧 愛讀書的趕緊收藏吧！·速讀技能一般運(yùn)用在四大方面
·成為“超級快速閱讀者”的秘訣是“循序漸進(jìn)”·英語速讀太難？別傻了，那是你沒技巧！
·5招練就快速閱讀本領(lǐng)，你一定要學(xué)會1招！·快速閱讀相關(guān)：漢字順序錯亂并不影響閱讀？
·家長必讀：兒童閱讀的20條實(shí)用建議·閱讀是學(xué)習(xí)之母
·速讀相關(guān)：增強(qiáng)意志力六法·閱讀質(zhì)量與數(shù)量的關(guān)系
·家長須知：學(xué)習(xí)習(xí)慣要在十歲之前養(yǎng)成·提升注意力和專注度的幾大好習(xí)慣
·導(dǎo)致速讀訓(xùn)練失敗的幾個細(xì)節(jié)問題·快速閱讀需要有千里眼
·快速閱讀的關(guān)鍵在于身心調(diào)整·學(xué)習(xí)快速閱讀，你要知道這十個原則！
·精確細(xì)讀法 ·教您選擇正確快速閱讀方法
·閱讀高難度材料的方法和經(jīng)驗(yàn)·學(xué)習(xí)的五種能力
·八種培養(yǎng)學(xué)習(xí)興趣的方法 ·精英特教你戰(zhàn)勝注意力渙散的方法
·古希臘人提高記憶力的方法·快速閱讀助你提升個人軟實(shí)力
·家長必看：30個讓孩子愛上閱讀的小妙招！·快速閱讀是考試的一把利器
·快速閱讀成為出國留學(xué)的一把利劍·關(guān)于快速閱讀的記憶訓(xùn)練
·教你戰(zhàn)勝拖延癥的方法·加強(qiáng)記憶力的七種方法
·人一生的“高度”取決于小學(xué)時代的閱讀能力·快速閱讀，應(yīng)該像水一樣
·快速閱讀的心靜與感覺把握·如何提高快速閱讀水平
·構(gòu)建自身“知識生態(tài)系”的四個技巧·你，真的會“讀”嗎？
·4大妙招讓快速記憶簡單起來·長時間集中注意力的11個方法
·怎么養(yǎng)成每天速讀的好習(xí)慣？·高考現(xiàn)代文閱讀之科技文的閱讀方法
·2015高考現(xiàn)代文閱讀答題技巧·突破專業(yè)書籍的閱讀策略
·有意記憶法·快速閱讀中無聲閱讀的四大誤區(qū)
·9個不正確的學(xué)習(xí)方法，你占幾個？·2015年高考生物復(fù)習(xí)基本方法技巧
·看完這篇文章，你覺得快速記憶還難嗎？·慢速閱讀法
·快速閱讀相關(guān):你之所以不快樂，是因?yàn)槟阕罱x書太少了·我是如何使用思維導(dǎo)圖做讀書筆記的
·瘋狂速讀記憶訓(xùn)練，讓你的大腦高速運(yùn)轉(zhuǎn)起來·高效閱讀三部曲
·怎樣提高英語閱讀能力·快速閱讀相關(guān)：科學(xué)的管理時間
·從“大樹理論”看速讀成功的“五大要素”·教你速記的小絕招
·你是個有主動學(xué)習(xí)意愿的人嗎？·快速閱讀相關(guān)：輕松速讀四步走
·速讀技巧：是什么拉了快速閱讀的后腿？·史上最強(qiáng)英語單詞抗遺忘記憶法
·學(xué)習(xí)快速閱讀、快速記憶，你需要知道這些·速讀的閱讀過程和回憶過程
·精英特七大絕招：如何提高晚上的學(xué)習(xí)效率？·思維導(dǎo)圖為什么一定要手繪？
·精英特讓你贏在起點(diǎn)，贏在終點(diǎn)·我的托福閱讀滿分解題經(jīng)驗(yàn)分享
·關(guān)于閱讀的一些思考 ·作為小編的我提倡快速閱讀
·使用思維導(dǎo)圖提升記憶力的兩大訣竅·我的一些速讀經(jīng)驗(yàn)
·精英特教懶人7種高效記憶方法·提高學(xué)習(xí)效率的六大訣竅
·教你在快速閱讀中抗外界干擾的方法·記憶力相關(guān)：讓大腦重獲年輕的7個方法
·“最強(qiáng)大腦”6招速成法·我的英語閱讀提速經(jīng)驗(yàn)談
·部位記憶法·睡眠記憶法
·學(xué)習(xí)中浪費(fèi)時間的6個不良習(xí)慣·名人學(xué)習(xí)十八法
·GRE詞匯記憶方法技巧·教你如何繪制思維導(dǎo)圖？
·新托福考試的三種快速閱讀技巧·專家解釋—人們對速讀的幾種誤解
·快速緩解眼睛疲勞的方法：易筋經(jīng)眼保健操 ·繪制思維導(dǎo)圖的六個基本原則
·快速緩解眼睛疲勞的幾個小方法·快速閱讀，慢速記憶
·看看哪種閱讀方法適合您！·快速閱讀的一般過程
·速讀訓(xùn)練四步走—用“視讀”取代“音讀”·怎樣高效記憶電腦鍵盤上的26個字母的順序
·關(guān)于快速閱讀的心態(tài)問題·快速閱讀相關(guān)：看猶太人是怎樣管理時間的
·兩個小故事談速讀訓(xùn)練·看美國是怎樣培養(yǎng)孩子的英語閱讀能力
·快速閱讀技巧實(shí)際運(yùn)用—退縮式閱讀法·我對提高閱讀速度的一些看法
·快速閱讀訓(xùn)練中的幾種呼吸方法·最實(shí)用的幾種鍛煉快速閱讀能力的方法
·不利于快速閱讀訓(xùn)練的兩種情況·如何用快速閱讀法閱讀教科書
·思維導(dǎo)圖教你把一本書變成一張紙·提升語文閱讀效率的方法
·快速閱讀技巧實(shí)際運(yùn)用—鑒別閱讀法·巧用框架式閱讀法 攻克四級閱讀理解長難句
·中學(xué)化學(xué)難點(diǎn)趣味記憶方法·快速閱讀相關(guān)：閱讀要掌握好方法
·珍惜時間的名言警句·快速閱讀訓(xùn)練方法五原則
·記憶訓(xùn)練可以實(shí)現(xiàn)的幾種境界·閱讀的重要性：好的英語是“讀”出來的
·用“閱讀圖”來節(jié)約更多時間·精英特教你十種保持記憶力超群的方法
·全腦速讀記憶訓(xùn)練有效嗎？·精英特教你十招記單詞的神奇記憶法
·“三步走”提高閱讀速度·快速閱讀是人類記憶進(jìn)化的必經(jīng)之路
·突破三個障礙，讓速讀為你的人生添彩·提高閱讀速度的簡單方法
·快速閱讀方法技巧-五步速讀法·記憶是智慧之母
·變速閱讀法·檢測快速閱讀訓(xùn)練效果的幾種方法
·雅思閱讀備戰(zhàn)良方：精讀和泛讀·網(wǎng)絡(luò)學(xué)習(xí)怎樣最有效？
·英語快速閱讀：四級快速閱讀解題兩步走·培養(yǎng)快速閱讀能力，給孩子裝上飛翔的翅膀
·速讀訓(xùn)練中為什么你總也記不住？·讓你的大腦越來越聰明的12個方法
·快讀閱讀方法訓(xùn)練：“字形解義”·快速閱讀技巧之直讀法
·暑假，如何讓孩子愛上讀書·擴(kuò)大視幅最高效的方法
·宮殿記憶法·現(xiàn)代高效閱讀法—快速閱讀
·為什么快速閱讀能力要盡早培養(yǎng)？·如何在快速閱讀文章的同時做筆記
·12個小技巧讓你愛上閱讀·閱讀目的決定閱讀方法
·快速閱讀的關(guān)鍵之眼睛·幾個簡單的小方法讓自己學(xué)會速讀和速記
·復(fù)習(xí)的法寶：四輪復(fù)習(xí)法·精英特給我的教學(xué)帶來的思考
·康奈爾筆記法·提高記憶力的最有效最簡單的方法
·給速讀新手們的一些建議·思維導(dǎo)圖中關(guān)鍵詞的選取
·三種最常用的記憶法 ·學(xué)會管理你的學(xué)習(xí)時間
·速讀訓(xùn)練要有清晰的目標(biāo)·視覺停留和快速閱讀的關(guān)系
·運(yùn)算記憶法·2014英語四六級快速閱讀部分臨考必讀策略
·2014英語四六級快速閱讀解題技巧·2014高考英語閱讀答題技巧與解題方法
·人類閱讀速讀極限是多少？·為什么你的速讀訓(xùn)練總也不成功？
·英語四六級復(fù)習(xí)誤區(qū)及應(yīng)對技巧·提高雅思閱讀速度的三個最有效方法
·學(xué)習(xí)思維導(dǎo)圖的六個技巧·提高雅思閱讀的七大高效法
·快速閱讀記憶相關(guān)：混合法記憶托福詞匯·雅思閱讀技巧介紹：快速閱讀法
·英語四六級閱讀高分突破“五步法”·在大腦里畫思維導(dǎo)圖
·如何掌握速讀中的記憶能力·提高速讀理解能力的幾個簡單方法
·2014年6月英語四六級閱讀理解高分突破技巧·開發(fā)眼睛的潛在能力 增強(qiáng)快速閱讀實(shí)力
·雅思閱讀解題方法大揭秘·我的高效率背誦六級單詞法
·速讀訓(xùn)練中擴(kuò)大視幅的誤區(qū)·速讀三放松，你做到了嗎？
·備戰(zhàn)2014英語四六級閱讀·淺談速讀中的兩個要點(diǎn)
·幾種有效的閱讀方法·記憶陌生單詞的小技巧
·橘子集中法帶你進(jìn)入閱讀理想狀態(tài)·連鎖記憶法
·英語快速閱讀：六大絕招讓你輕松搞定閱讀速度·速讀應(yīng)該使用什么樣的書籍練習(xí)
·提高閱讀速度的自我訓(xùn)練方法·大腦能轉(zhuǎn)多快，我們的閱讀就能讀多快
·快速閱讀之實(shí)物書籍閱讀訓(xùn)練過程·時間管理：四象限法
·突破雅思考試閱讀瓶頸的2大方法·保持速讀精力充沛的生活好習(xí)慣
·比喻記憶法·PQ4R學(xué)習(xí)法
·閱讀繪本有助培養(yǎng)孩子觀察力·雅思閱讀提速法寶：平行法
·托福閱讀速度的提高方法·法律常識記憶順口溜
·我參加快速閱讀訓(xùn)練的心得體會·SAT閱讀之快速閱讀技巧
·每天25分鐘提高工作效率·根特的集中注意訓(xùn)練法
·自己如何在快速閱讀訓(xùn)練中克服懶惰·快速閱讀技巧之整體閱讀法
·成為思維導(dǎo)圖高手的24個習(xí)慣 ·速讀訓(xùn)練六種境界
·淺談快速閱讀的好處·高中生物記憶方法
·12種簡便的記憶方法·如何在雅思考試中有效運(yùn)用略讀和尋讀做閱讀
·英語快速閱讀：兩步猜詞義，迅速提高考研英語閱讀能力·GRE快速閱讀常見的誤區(qū)
· 怎樣提高GRE閱讀速度·精英特教你如何提高閱讀速度
·GRE的快速閱讀勢在必行·雅思閱讀臨場小技巧
·26條時間管理技巧· 尖子生名列前茅的十大秘訣
·理解閱讀法·巧記“三十六計”
·快速閱讀是突破孩子閱讀瓶頸的法寶·巧記多音多義詞
· 聽時間走路的聲音·雅思快速閱讀技巧大公開
·十步閱讀法·快速閱讀技巧實(shí)際運(yùn)用-略讀法
·中考閱讀理解技巧點(diǎn)撥 · 語文課堂教學(xué)中高效閱讀訓(xùn)練的方法
·歷史時間記憶法·SAT考試閱讀滿分800備考經(jīng)驗(yàn)談
·記憶堵塞怎么辦· 小學(xué)生閱讀指導(dǎo)方法
·小技巧有助小孩子養(yǎng)成快速閱讀的習(xí)慣·生活中的記憶術(shù)
·英語快速閱讀：SAT五大高分策略·速讀相關(guān)：改變15種壞習(xí)慣提高您的幸運(yùn)值
·英語快速閱讀：SAT長篇文章閱讀的技巧·英語快速閱讀：SAT備考分析
·速讀相關(guān)：如何畫時間管理分布圖·英語快速閱讀：找到托福考試中提高閱讀能力的方法
·速讀相關(guān)：從生活習(xí)慣的提高注意力·英語快速閱讀：雅思考試中的閱讀水平提高
·英語快速閱讀：SAT三年學(xué)習(xí)計劃·速讀相關(guān)：興趣成就時間管理
·英語快速閱讀：考研英語閱讀速度如何突破·快速閱讀相關(guān)：如何培養(yǎng)小學(xué)生語文素養(yǎng)
·快速閱讀相關(guān)：中學(xué)數(shù)學(xué)閱讀應(yīng)該請注意的問題·英語快速閱讀：(CET-4)英語四級快速閱讀技巧
·英語快速閱讀：英語六級考試中的如何提高閱讀效率·英語快速閱讀：出國考雅思需要快速閱讀
·英語快速閱讀：出國考托福需要的三種快速閱讀技巧·快速閱讀相關(guān)：我的二十七招節(jié)省時間
·快速閱讀相關(guān)：為什么需要工作進(jìn)度表·快速閱讀相關(guān)：如何提高工作資料閱讀效率
·快速閱讀相關(guān)：掌握時間法則·快速閱讀相關(guān)：學(xué)會如何把握90分鐘的時間
·快速閱讀相關(guān)：休閑與高效工作學(xué)習(xí)的良性循環(huán)·快速閱讀訓(xùn)練相關(guān)：10個最有效的時間管理方法
·快速閱讀技巧實(shí)際運(yùn)用-掃讀法·快速閱讀技巧實(shí)際運(yùn)用-跳讀法
·快速閱讀訓(xùn)練后緩解眼睛疲勞的遠(yuǎn)眺圖·快速閱讀技巧實(shí)際運(yùn)用-猜讀法
·快速閱讀訓(xùn)練中緩解眼睛疲勞的方法·快速閱讀入門的幾個簡單技巧
·快速閱讀訓(xùn)練：如何養(yǎng)成良好的習(xí)慣·從李嘉誠演講看快速閱讀訓(xùn)練中應(yīng)注意的品質(zhì)
·從習(xí)慣養(yǎng)成的角度談快速閱讀訓(xùn)練·快速閱讀等三種讀書方法
·中外關(guān)于讀書的名人名言·學(xué)習(xí)效率的自我評價與自我改進(jìn)
·提高英文閱讀速度的九種決竅·學(xué)習(xí)時如何集中注意力
·提高效率的十個方法·英語四六級備考：英語快速閱讀四大法則
·高效學(xué)習(xí)“五部曲”·幾種改善視力的訓(xùn)練方法
·中學(xué)生如何提高寫作能力·淺談?wù)Z文教學(xué)中學(xué)生閱讀能力的培養(yǎng)
·中學(xué)歷史記憶方法·十種可清醒頭腦的大腦體操
·政治學(xué)科十大記憶方法·地理知識趣味記憶方法
·化學(xué)記憶方法·英語快速閱讀的方法和技巧
·五個方法練習(xí)你的注意力和觀察力·艾賓浩斯記憶曲線
·損害記憶力的外界因素·維克斯健腦操
·你知道腦電波嗎？·相貌姓名記憶法
·歸類記憶法·理解記憶法
·觀察記憶法·提綱記憶法
·諧音記憶法·怎樣提高記憶力
·快速閱讀中的五忌·必須克服的10種不良閱讀習(xí)慣
·李白讀書法·自我訓(xùn)練速讀八法
·閱讀的基本技巧——4S讀書法·你知道你的的閱讀習(xí)慣嗎？
·培養(yǎng)快速閱讀好習(xí)慣·快速閱讀要堅(jiān)持“十要”
·快速閱讀四大法則·高效速讀記憶的好處
·高效速讀是現(xiàn)代人的生存方式

Copyright © 2005-2021 www.mxjqw.com All Rights Reserved
昆明精英特科技開發(fā)有限公司 版權(quán)所有
地址：昆明市西山區(qū)環(huán)城南路675號汕頭大廈B座19樓06號
客服熱線：4008129365, 0871-64636969, 64636148, 64836684
QQ: 309900083。點(diǎn)擊即可與速讀咨詢老師進(jìn)行QQ對話。 QQ: 409768611。點(diǎn)擊即可與速讀咨詢老師進(jìn)行QQ對話。
網(wǎng)站備案號：滇ICP備05003416號   
查看值班客服……